roundheadedboy

สารบัญ
การคูณสามารถเขียนได้หลายรูป โดยที่ความหมายยังคงเดิม ด้านล่างทั้งหมด คือ 5 คูณ 2
$5times 2$
$5cdot2$
$(5)2, 5(2), (5)(2), 5[2>, [5]2, [5][2]$ $5*2$
สำหรับเครื่องหมายดอกจัน (*) นิยมใช้ในคอมพิวเตอร์ เพราะเป็นสัญลักษณ์ที่มีในทุกแป้นพิมพ์ แต่เราไม่ใช้ในการเขียนด้วยมือ และเราจะใช้ก็ต่อเมื่อไม่มีเครื่องหมายอื่นมาทดแทน (การใช้เครื่องหมายนี้เริ่มมาจากภาษาคอมพิวเตอร์ฟอร์แทรน) สำหรับตัวแปร โดยปกติแล้วเราจะไม่เขียนสัญลักษณ์การคูณไว้ นี่คือมาตรฐานในพีชคณิต
5x และ xy.
ประโยคสัญลักษณ์นี้อาจก่อให้เกิดการสับสน เวลาตัวแปรมีชื่อยาวกว่าหนึ่งตัวอักษร และการเขียนลักษณะนี้จะไม่ใช้กับเลขโดดสองตัว เช่น 52 ไม่สามารถแปลว่า 5 × 2. ได้
ถ้าพจน์แต่ละพจน์ของผลคูณไม่ได้เขียนออกมาทั้งหมด เราอาจจะใช้เครื่องหมายจุดไข่ปลาแทนพจน์ที่หายไป เช่นเดียวกับการดำเนินการอื่นๆ (เช่น การบวก) เช่น ผลคูณของจำนวนธรรมชาติ ตั้งแต่ 1-100 อาจเขียน $1 cdot 2 cdot ldots cdot 99 cdot 100$ . และสามารถเขียนให้เครื่องหมายจุดไข่ปลาอยู่บริเวณกึ่งกลางแนวตั้งของแถวได้อีกด้วย คือ $1 cdot 2 cdot cdots cdot 99 cdot 100$ .
นอกจากนี้แล้ว ผลคูณยังสามารถเขียนได้ด้วยเครื่องหมายผลคูณ ซึ่งมาจาก อักษร Π (Pi) ตัวใหญ่ ในอักษรกรีก. ตัวอย่างเช่น
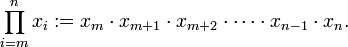
$prod_{i=m}^{n} x_{i} := x_{m} cdot x_{m+1} cdot x_{m+2} cdot cdots cdot x_{n-1} cdot x_{n}.$
ตัวห้อยของประโยคสัญลักษณ์ข้างต้นแทนตัวแปรหุ่น (สำหรับประโยคนี้คือ i) และขอบเขตล่าง (m); ตัวยกแทนขอบเขตบน (n) เช่น
$prod_{i=2}^{6} left(1 + {1over i}right) = left(1 + {1over 2}right) cdot left(1 + {1over 3}right) cdot left(1 + {1over 4}right) cdot left(1 + {1over 5}right) cdot left(1 + {1over 6}right) = {7over 2}.$
เรายังสามารถหาผลคูณที่มีพจน์เป็นอนันต์ได้อีกด้วย เรียกว่าผลคูณอนันต์ ในการเขียน เราจะแทนที่ n ด้านบนด้วยเครื่องหมายอนันต์ (∞). ผลคูณของพจน์จะกำหนดด้วยขีดจำกัดของผลคูณของ n พจน์แรก โดย n เพิ่มขึ้นโดยไม่มีขอบเขต เช่น
$prod_{i=m}^{infty} x_{i} := lim_{ntoinfty} prod_{i=m}^{n} x_{i}$
นอกจากนี้ยังสามารถแทน m ด้วยจำนวนลบอนันต์
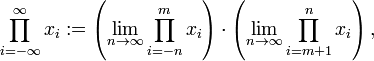
$prod_{i=-infty}^infty x_i := left(lim_{ntoinfty}prod_{i=-n}^m x_iright) cdot left(lim_{ntoinfty}prod_{i=m+1}^n x_iright),$
และสำหรับจำนวนเต็ม m บางจำนวน สามารถกำหนดได้ทั้งอนันต์และลบอนันต์

สัญลักษณ์
สำหรับความหมายของการคูณ ผลคูณของจำนวนธรรมชาติ n และ m ใดๆ
$mn := sum_{k=1}^n m$
กล่าวสั้นๆ คือ 'บวก m เข้ากับตัวเอง n ตัว' สามารถเขียนได้ในลักษณะนี้เพื่อให้ชัดเจนมากขึ้น
m × n = m + m + m + ... + m
หมายถึงมีจำนวน 'm' n ตัวบวกกันนั่นเอง
โดยใช้นิยาม เราสามารถพิสูจน์สมบัติของการคูณได้โดยง่ายดาย โดยดูจากสองตัวอย่างข้างต้น เรามีสมบัติว่า จำนวนสองจำนวนที่คูณกันสามารถสลับที่กันได้โดยผลคูณยังคงเดิม เราเรียกสมบัตินี้ว่า สมบัติการสลับที่ และ สมบัตินี้เป็นจริงสำหรับจำนวน x และ y ใดๆ นั่นคือ
x · y = y · x.
นอกจากนี้ การคูณยังมีสมบัติการเปลี่ยนหมู่อีกด้วย ความหมายสำหรับจำนวน x,y และ z ใดๆ คือ
(x · y)z = x(y · z).
หมายเหตุจากพีชคณิต: เครื่องหมายวงเล็บ หมายถึง การดำเนินภายในวงเล็บจะต้องกระทำก่อนการดำเนินการภายนอกวงเล็บ
การคูณมีสมบัติการแจกแจง เพราะ
x(y + z) = xy + xz.
มีสิ่งที่น่าสนใจเกี่ยวกับการคูณกับ 1 นั่นคือ
1 · x = x.
เราเรียก 1 ว่า จำนวนเอกลักษณ์
สำหรับเลข 0 เราจะได้
m · 0 = m + m + m +...+ m
เมื่อเรานำ '0' m ตัวมาบวกกัน ผลลัพธ์ที่ได้ย่อมเป็นศูนย์ นั่นคือ
m · 0 = 0
ไม่ว่า m จะเป็นจำนวนใด (แม้กระทั่งอนันต์).
การคูณกับจำนวนลบอาจจะต้องมีการคิดเล็กน้อย เริ่มจากการคูณ (−1) กับจำนวนเต็ม m ใดๆ
(−1)m = (−1) + (−1) +...+ (−1) = −m
นี่เป็นความจริงที่น่าสนใจว่า จำนวนลบ คือ จำนวนลบหนึ่ง คูณกับจำนวนบวกนั่นเอง เพราะฉะนั้นผลคูณระหว่างจำนวนบวกกับจำนวนลบทำได้โดยการคูณปกติ แล้วคูณด้วย (−1)
(−1)(−1) = −(−1) = 1
ในขณะนี้ เราสามารถสรุปการคูณระหว่างจำนวนเต็มสองจำนวนใดๆ ได้แล้ว และนิยามนี้ยังขยายไปสำหรับเซตของเศษส่วน หรือ จำนวนตรรกยะ และขยายไปถึงจำนวนจริงและจำนวนเชิงซ้อน
หลายคนอาจสงสัยถ้าบอกว่า ผลคูณของ'ไร้จำนวน' คือ 1
รูปแบบนิยามเรียกซ้ำของการคูณเป็นไปตามกฎ
x · 0 = 0
x · y = x + x·(y − 1)
เมื่อ x เป็นจำนวนจริง และ y เป็นจำนวนธรรมชาติ เมื่อเรากำหนดนิยามของการคูณจำนวนธรรมชาติแล้ว เรายังขยายผลไปถึงจำนวนเต็ม จำนวนจริง และจำนวนเชิงซ้อนได้

5 × 2 = 5 + 5 = 10
2 × 5 = 2 + 2 + 2 + 2 + 2 = 10
4 × 3 = 4 + 4 + 4 = 12
m × 6 = m + m + m + m + m + m

นิยาม
สำหรับวิธีที่รวดเร็วเพื่อคำนวณผลคูณของจำนวนขนาดใหญ่ ดู อัลกอริทึมการคูณ
ถ้าต้องการคูณจำนวณโดยใช้กระดาษกับดินสอ คุณจะต้องใช้สูตรคูณ (ไม่ว่าจะอยู่ในกระดาษหรือสมองของคุณ) และคุณอาจต้องรู้อัลกอริทึมการคูณอีกด้วย

ในทางดนตรี

การคูณอย่างง่าย
ส่วนกลับ
สูตรคูณ